AIデータ分析コラム【8】機械学習の物理学への応用　～機械学習で物理現象の理解を加速～

深層学習をはじめとする機械学習技術の進歩はめざましく、様々な分野で最高性能(State-of-the-Art)を塗り替える機械学習モデルが次々と開発されています。これらのモデルの多くは、オープンソースとして公開されており、計算機環境さえ準備すれば、機械学習の専門家でなくても最先端の技術を利用することができます。このような背景から、近年、物理学の様々な分野において機械学習の応用が急速に進んでいます。

機械学習を物理学に応用する場合、モデルの予測精度だけでなく、なぜそのような予測結果をモデルが出力したかという理由が分かること、つまりモデルの解釈性が非常に重視されます。この点は、画像認識や音声認識、自然言語処理など、これまで機械学習が得意としてきた分野への応用とは異なっています。

本コラムでは、物理学に応用されている機械学習モデルの中から解釈性の高い2つのモデルを紹介します。

なお、説明のため数式を使っていますが、苦手な方は数式部分を読み飛ばしていただいて問題ありません。大まかな流れを感じていただければ幸いです。

Physics-informed neural networks (物理法則に基づくニューラルネットワーク)

物理法則には、常微分方程式や偏微分方程式で表されるものが多くあります。これらは、解析的に(式の変形で)解けないものが多く、差分法などの数値計算によって近似解を逐次的に求めていきます。しかし、近似精度の高い解を得るには長時間の計算と多くの計算リソースが必要です。この計算負荷を軽減する機械学習モデルとして、Physics-Informed Neural Networks(PINN)[1]が提案されています。

通常、ニューラルネットワークの学習では、学習データと予測値の乖離量を損失関数とし、損失関数の値が小さくなるようにネットワーク内のパラメータを調整していきます。PINNでは、この損失関数に微分方程式からの乖離量を加えることで、微分方程式の解を出力するモデルを学習していきます。

編集部注：「損失関数」とは、機械学習においてモデルが算出した予測結果と実際の正解のズレを計算するための関数のことです。このズレが小さいほど良いモデルといえるため、モデルをよりよくする(最適化といいます)ための指標として使われます。

PINNでBurgers方程式を解く

一例として、流体力学で用いられるBurgers方程式を使って説明します。

Burgers方程式：

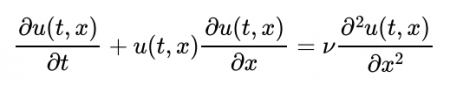
ここで、tは時間、xは空間座標を表し、u(t,x)はtとxの関数になっています。また、νは流体の性質に依存する定数です。文献[1]では、Burgers方程式を解くPINNとして、全結合型のニューラルネットワークを提案しています。

このネットワークは、任意の時間tと空間座標xにおけるu(t,x)を高速に計算することができます。損失関数における微分方程式からの乖離量は、微分方程式の左辺と右辺の差を2乗した値とし、任意の時間と空間座標の組み合わせ(N個)に対して計算します。

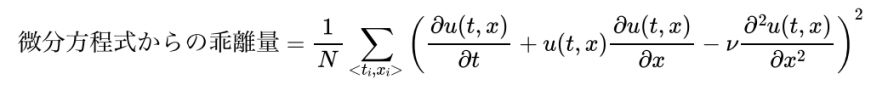
右辺の各微分項は、ニューラルネットワークの自動微分機能によって計算することができます。自動微分機能は、通常のニューラルネットワークのパラメータ調整で使われており、TensorFlowやPyTorchなどのメジャーな深層学習フレームワークで既に実装されています。

潜在能力は高い、だが、さらなる発展に期待

PINNは、微分方程式からの乖離量をモデルの学習に導入することで、解釈性の高い機械学習モデルとなっています。そして、従来の数値計算に比べて少ない計算負荷で高精度の解を短時間で計算することができます。

一方、境界条件(Burgers方程式では流体容器の端でのuの値)と初期条件(uの初期値)を学習データとして与える必要があるため、これらの条件が変わる場合にはモデルを再学習する必要があります。また、物理法則の損失関数への取り込み方によっては、モデルの学習が収束しないことが報告されています。

編集部注：「モデルの学習が収束しない」とは、機械学習においてモデルが予測値を算出できるようにならないことをいいます。モデルは最適解を目指して計算をしますが、最適解を見つけた判断ができずいつまでも計算を続けている状態になることです。

Symbolic Regression Model (記号回帰モデル)

PINNでは、現象を支配する物理法則として微分方程式が陽に与えられていました。一方、実験等のデータから物理量間の関係式を推定するSymbolic Regression Modelの開発も活発に行われています。例えば、万有引力の法則の場合、関係式は、

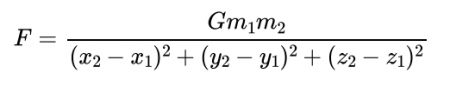
となり、データは重力FとG, m1, m2, x1,…,z2の10個の物理量の値の組み合わせになります。物理量間の関係が数式で推定されるため、Symbolic Regression Modelは極めて解釈性の高い機械学習モデルです。

関係式の推定は、目的とする物理量(目的変数)を他の物理量(説明変数)で表現した未知の関数をデータから求めることから、逆問題と言われています。この問題を解くためには、説明変数となる物理量と＋×等の演算子を組み合わせて近似式を作り、与えられたデータをうまく近似できるような近似式を探索していく必要があります。しかし、物理量や想定する演算子の数が増えると、探索する近似式の数が指数関数的に増大します。そこで、組合せ最適化アルゴリズムの一つである遺伝的アルゴリズムを使った近似式探索が広く行われています。

編集部注：「逆問題」とは、数学や物理において結果・観測値(出力)から原因(入力)を推定する問題のことをいいます。反対に、入力から出力を推定する問題を順問題といいます。上述の万有引力の例は、万有引力に関わる観測結果から万有引力の法則(原因)を推定する逆問題です。

機械学習でファインマン物理学

AI Feynman[2]は、物理的な制約とニューラルネットワークを使って最適な近似式を探索するSymbolic Regression Modelです。このモデルは、近似式の探索と探索問題の簡易化を再帰的に行い、最適な近似式を求めます。様々な分野で広く使える遺伝的アルゴリズムを使ったSymbolic Regression Modelと異なり、AI Feynmanは物理的な制約をアルゴリズムに加えているため、物理に特化したSymbolic Regression Modelになります。

AI Feynmanの近似式の探索では、

▪️近似式の両辺で物理量の単位は同じになる。
▪️近似式は簡単(低次元)な多項式で表現される。

などの物理的な知見・経験則を満たす近似式を総当たり的に探索していきます。この段階で近似式を発見できない場合、次のような探索問題の簡易化を行います。

▪️説明変数となる物理量の数を削減する。例えば、前述の万有引力の法則では、新しい物理量：x=x2-x1、y=y2-y1、z=z2-z1を導入すれば、物理量の数を減らすことができます。
▪️近似式を2つの項に因数分解し、より小さい探索問題に分割する。

そして、簡易化した探索問題に対して、再び近似式の探索を行います。探索問題の簡易化が可能かどうかは、データで学習したニューラルネットワークを使って確認します。

ノーベル物理学賞を受賞したリチャード・ P・ファインマンの物理学講義から選ばれた100個の基本的な物理法則について、これらをデータから発見する実験が行われました。遺伝的アルゴリズムによるモデルが71%の法則を発見したのに対し、AI Feynmanはすべての法則を発見しました。

理解から創造へ

Symbolic Regression Modelで得られる関係式は、学習時に与えられたデータの近似式に過ぎず、物理法則とは言えないかも知れません。また、データが変われば関係式は成り立たなくなる可能性もあります。しかし、物理量間の関係が定量的に表現されることで、物理現象の理解を深めることができます。さらに、得られた関係式からアイデアが生まれ、新しい理論の創造につながる可能性もあります。

共進化する物理学と機械学習

ハードウェアの進化と相まって、高性能な機械学習モデルが今後も開発されていくでしょう。一方、スーパーコンピュータを使った物理法則に基づく数値シミュレーションもかなりの精度で実験を再現できるようになってきています。数値シミュレーションと機械学習の融合が今後さらに進み、物理学と機械学習の双方においてブレイクスルーが起きることが期待されています。

参考文献

1.Raissi, Maziar, Paris Perdikaris, and George Em Karniadakis. "Physics informed deep learning (part I): Data-driven solutions of nonlinear partial differential equations." arXiv preprint arXiv:1711.10561 (2017).
2.Udrescu, Silviu-Marian, and Max Tegmark. "AI Feynman: A physics-inspired method for symbolic regression." Science Advances 6.16 (2020).