- データ分析現場の苦労と切望から -

はじめに

AIや機械学習がメディアで華々しく取り上げられ、データ分析へのお客様からの期待が大きくなってきました。ご相談頂く内容は多種多様（ロングテール）となり、おおよそ初見の課題となる傾向にあります。課題解決の道を探るための時間や費用はごく限られていて、できるだけ早く課題の解決に向けた見通しを立てる必要があります。そのためには課題のポイントを見極めて、かつ、そこで、優れたパフォーマンスを示す手法について、速やかに見通しを得る必要があります。

新規の課題で高いパフォーマンスが得られる場合、それは、なんらかの発見が伴う研究の成功に他ならない、という過去の事実に照らすと、ちょっと考えられないような状況です。事実、データ分析の道具（手法やモデル）は随分と複雑で多様になってきました。そして、高性能な結果が出ている道具だからと言って、期待通りのパフォーマンスを自分の課題で出せる保証はありません（ノーフリーランチ定理_[1]）。それでも、この状況に対応していくことが、データ分析を生業とする現場の技術者に求められているように感じています。

どうすれば、課題解決の見通しが早期に得られるのでしょうか？また、如何にして、道具の高い能力を引き出すことができるのでしょうか？このコラムでは、少しそういう話をしたいと思います。

AutoMLではなく汎用的知識

モデルと課題のマッチングといえば、AutoMLを思い起こす方が多いと思います。沢山のモデル候補があって、データを使って、もっとも成績の良いモデルを選ぶというものです。分析の一部分としてAutoMLを使ってみることは、有益な場合があります。しかし、AutoMLがあれば良いという課題にはあまり出会いません。というのも、AutoMLで解ける課題であるということは、既にモデルの性能の優劣を正しく評価する方法が得られていることを意味するからです。これはデータ分析としては既にメインの工程が終わっていることを意味しています。実際、ある性能評価方法が策定されていて、これを用いてモデルデザインをコントロールできる段階まで課題の検討が進んでいることになります。

性能評価方法の策定が簡単でない課題は沢山あります。典型的なのは異常検知です。通常は異常データが少ないため、検知モデルが異常を見逃す確率が評価できません。また、あまり知られてないかもしれませんが、時系列予測もそのような例です。モデルが予測に成功していることは直ぐに分かります。しかしながら、予測に失敗したときには、モデルに問題があって改善すべきなのか、そもそも予測できないデータなのかの判断が必要ですが、これには立ち入った分析が必要になります。

また、ここが重要なのですが、モデルやアルゴリズムなどの何らかの数学的な道具立てが実際の課題で有効になる、という評価をあらかじめ結論する際は、なんらかの前提、仮説または既に確立された法則を利用する必要があります。この利用されている前提等を明示することは、実際の適用時のリスクを明らかにする上で必要なポイントで、データ分析が果たすべき重要な役割です。複雑なモデルでは、適用結果だけを見ても、どのような前提等を利用した結論なのか分かり難く、リスクが隠れやすい傾向にあります。

それでは、どうやってこれらの課題に対応して行くのでしょうか？ 

昨今、汎用ＡＩの可能性を耳にするようになりましたが、考え方は近いものです。つまり、課題とモデルの分析に汎用的に利用できる考え方や方法をできるだけ利用します。以下では、課題解決に向けて汎用的に有用性があると考えられる知識について、その一部をご紹介します。

課題の難易を捉える

まずは、解決すべき問題・課題の難易、特に難しさのポイントを捉えます。問題・課題は常に望み通りに解けるとは限りませんが、その難しさはおよそ捉えられます（図１）。これは、おおよそ、複雑さと課題とのかかわり方を捉えることとも言えます（図２）。

図１．課題の難易は捉えられる

図２．課題と複雑さの関係を捉える

例えば検知問題では、検知対象の信号の強弱と検出の妨げになるノイズの強弱が基本的な難易となりますが、信号とノイズの強弱の観点で難しい場合が重要です。この時、弱い信号の増強や強いノイズの抑制が必要となり、それぞれの複雑さが課題の難易を左右します。

コントロールの観点

ところで、ひと口に「課題状況」と申しましたが、これを捉えるための汎用的な考え方があります。実は殆どの問題や課題は、（広く解釈した）コントロール、またはその部分の問題として捉えられます。つまり、連続または不連続な選択肢が存在して適切に調整・選択することは、広い意味でコントロールと言えます。そしてコントロールのパフォーマンスを優れたものにすることが、課題そのものまたは課題の直接的な背景や動機となっています（図３）。例えば、予測や状況判断（検知・認識）等の課題は、これらを用いるコントロールの結果をより優れたものとするために生じています。

図３．選択肢とその選択が問題

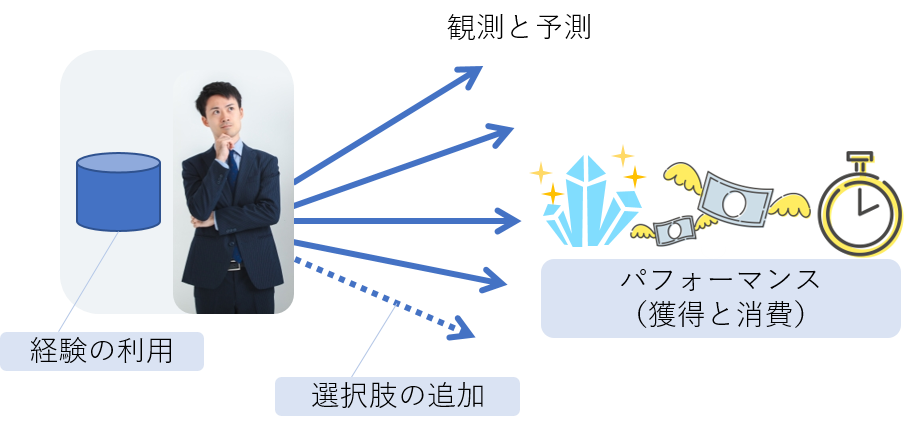
課題状況を捉えて課題の全体像が見えて来ると、複雑さと課題の関わりがより明確になり、課題の難易や解決への道筋が捉えやすくなります。例えば、人間が複雑なプロセスに関わって性能が左右されるようなシステムでは、人間とプロセスそれぞれの異質な複雑さと性能が関わっています。性能と複雑さの関わりが捉えられれば、性能を保って複雑さの性能への関与を抑制することで、問題の解決や課題の難易度を抑制するというシナリオに繋げられます。

ちなみに、（広義の）コントロールの観点は、思いのほか強力な汎用性があります。生物、技術、社会の進化を説明し、私たちが感覚や記憶を備える理由や、言語、貨幣の働き等を説明します。実際、コントロール能力が優れることが、強い適応能力を説明します。また、観測や経験の活用がコントロール能力において決定的に重要である点が、人間と社会の機能的な要素の存在を良く説明します。なお、人・モノ・カネなどの資源は選択肢の維持・拡大として、コントロールの枠組みにおいてその働きを解釈できます。

さらに、データ分析業務の対象として重要な、人によってデザインされたシステム（人工システム）について、いわゆる物理現象と異なる特徴と複雑さを理解する考え方が、コントロールの観点から得られます。すなわち、（力学の基本法則に従うような）物理現象では未来が決まっていますが、人はコントロールを通じて未来を選び望む結果に向けて変えようとします。この人の特性を反映することで、人工システムはその役割を果たしています。

シンギュラリティ

局所最適化と関係性の形成

人工システムや人間行動の振る舞い（選択肢の選択）は、まったくデタラメではなく、何らかの関係または関係性の下にあります。機械学習の多くは、この関係性をデータからモデルに抽出します。人間に由来する類の関係性については、コントロールの観点から、これが生じる仕組みを説明できます。それが局所的な最適化です。

人工システムや人間は、選択肢を選択できるわけですが、認識できる範囲、必要な努力、期待される効果等に限定された範囲で（局所的）、より望ましい選択肢が選択されます。望ましい結果となる選択は、コントロール系の内部（記憶）または外部（設計や周囲との関係性）に組み込まれて、振る舞いに関係性を生じます（最適化）。

システムが複雑になると、選択の揺らぎが大きくなりますが、局所最適化は引き続き有効な観点です。実際、人間の行動にも局所最適化がしっかりと働いていて、適応行動_[3]として、古くから研究されてきました。人間の行為・行動に関わる大規模データの学習が上手く行くケースは、適応行動の構造や特性にマッチしたモデルや手法と言えます。

ちなみに、最適化の考え方は、物理現象を理解し振る舞いを支配する法則を捉えるための伝統的な原理の一つです_[4]。人工システムや人間行動と同一の考え方が当て嵌まることは興味深い点で、強力な汎用性を示唆します。一方で、ここで言う関係性は、動き（可能な選択肢の選択や想定しうる変化の中の実現）を規定・統制するものという、短時間的な意味で用いています。局所最適化の下での振る舞いが積み重なって、より長時間の関係性や構造が形成され、短時間の振る舞いにも関与して複雑になりうることは注意すべき点です。人の適応行動の結果として、クラスタが形成されるのは、そのような例の典型です。より一般的には、自己組織化と呼ばれる現象が当て嵌まります。

2種類の振る舞い方

機械学習の多くは、対象の局所最適化やその積み重ねに伴って生じている関係性をデータからモデルに抽出し、これを「学習」と称しています。従って、関係性の構造や特徴がモデルマッチングのポイントとなります。複雑な関係性の特徴を捉えるために汎用的に利用できる観点として、相互作用における2種類の振る舞い方（動き方）があります。

相互作用（の関係）とは着目している要素の動きとその周囲の動きの相互の影響関係を意味するもので、選択肢選択等の振る舞いに限りません。私たちを取りまく世界を観察すると、相互作用にはしばしば2種類の振る舞い方が伺われ、関係性の骨格と密接に関わっていることがわかります。この2種類の振る舞い方を足場として複雑さを捉える考え方は、一定の汎用性があると考えられます。

一つの種類は、低自由度で強い動き・振る舞い方、もう一つは高自由度で弱い動き・振る舞い方です。この２種類の振る舞い方は対照的な特徴を備え、しばしば相互に関連しつつ対となって生じます。物理現象、生物、人間行動、社会、さらにはモデル側となる数学に渡って広くかつ基礎的なものとして出現します。

まず、身近な例で見て行きます。身の回りで、モノを掴んで空間を少し移動させます。その際に物体（モノ）の運動自身（低自由度で強い動き）と、物体の運動が物体をとりまく周囲の空間に及ぼす影響（高自由度で弱い動き）が生じています（図４）。これは物理的な例ですが、類似する状況で、認知的な2種類の振る舞いが認められます。例えば、物体を机の上に置いて、その形状を指先で触れて認識することを考えます。手を動かすと明確な形状が脳裏に浮かびます。ここで手の動きを止めて手と物体が触れたまま別の手で物体側を動かすと、物体形状の知覚は消失し、物体に触れている手や指自身が知覚されます。手指と物体の間にはモノの空間移動と類似した相互作用が生じていて、２種類の動きが伴っています。手指が動く能動的関係と物体が動く受動的関係では、２種類の振る舞い方が切り替ります。これに伴って、対象の認識や身体の隠蔽が不連続に生じていることが分かります。

図４．身近にある2種類の振る舞い方

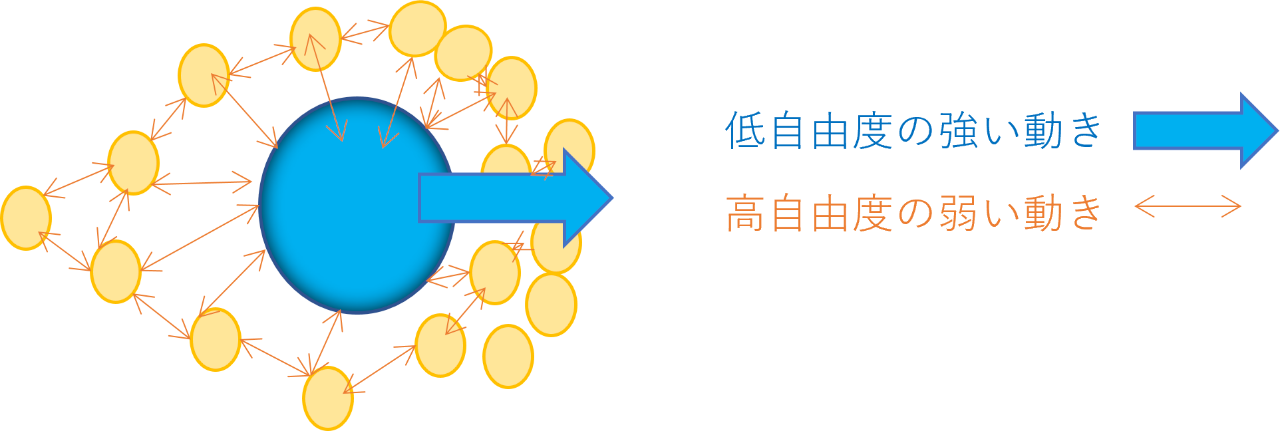
上の例は、この2種類の振る舞い方に注目することで、複雑な振る舞いや関係性に構造や特徴が見出しうることを示しています。このようにして捉えられる課題側の構造をモデル側の数学的な構造と結びつけることで、モデルマッチングが可能となってきます。重要なのは、「低自由度強挙動ー高自由度弱挙動」の観点に汎用性がある点です。そこで、関連する例を分野横断的にあげてみます。物理で言えば、粒子と場、乱流と層流、力学系のカオス的遍歴_[5]（低次元）と非対称運動_[6]（高次元）などがあげられます。生物では、近接した周囲の環境と複雑に結びついて安定的に振る舞う活動と、周囲との結びつきから離れてシンプルで不安定に振る舞う活動として一般的に見られます。基本的な例として植物と動物の生態があげられます。人の行動では、能動的行動と受動的行動に2種類の振る舞い方の特徴が見られます。自律神経系の交感神経、副交感神経は関連する対となる振る舞いの例です。また、運動的・認知的な行動の多くは、上述のように2種類の振る舞い方と関連します。社会組織では、関係性のグラフに影響として現れます。中心からの強いコントロールや影響を受ける集中的・階層的関係性（アソシエーション）と、局所的で密な関係性に基づくコミュニティが関連する2種類としてあげられます。新技術の普及過程_[7]や、サービスの利用行動にも関連が認められる２つの行動類型が見られます。

一方で数学では、２種類の振る舞い方が様々な概念に様々なかたちで組み込まれています。モデル作成の観点からは基本的なものとして、骨格（主成分）とノイズの区分、外挿向きの関数セットと内挿向きな関数セットの区別（層の概念_[8]を用います）があげられます。なお、簡単に見えて2者の関係が酷く難解な例として、自然数の掛け算と足し算があります。

低自由度強挙動ー高自由度弱挙動に共通する傾向のあるイメージとして、動と静があります。また、機能的な特性として大雑把な効率性と非効率な緻密さがあげられ、相互補完的な働きが伺われます。

おわりに

ＡＩや機械学習では、モデルが複雑になってきたせいか、それをしっかりとコントロールする方法が提供されない傾向にあります。私は、モデルが高い性能を生じる仕組みを性能機序と呼んでいます。性能機序を基に、モデルをコントロールすることを推奨し、また目指しています。そのためには課題とモデルの双方を分析するための汎用的方法が肝要と考えて、これを整備しつつ性能機序とお客様課題の分析に携わっています。

参考文献
[1]https://ja.wikipedia.org/wiki/ノーフリーランチ定理 (2023/12/27 閲覧).
[2]https://ja.wikipedia.org/wiki/特異点_(数学) (2023/12/27 閲覧).
[3]https://en.wikipedia.org/wiki/Adaptive_behavior (2023/12/27 閲覧).
[4]アーノルド, V.I. (著), 安藤, 蟹江, 丹羽 (訳), 古典力学の数学的方法. 岩波書店, 1980.
[5]金子, 津田, 複雑系のカオス的シナリオ. 朝倉書店, 1996.
[6]Shinjo, K., Sasada, T., Hamiltonian systems with many degrees of freedom: Asymmetric motion and intensity of motion in phase space, Phys. Rev. E 54, 4685, 1996.
[7]Shimogawa, S., Shinno,M., Saito, H., Structure of S-shaped growth in innovation diffusion, Phys. Rev. E 85, 056121, 2012.
[8]https://ja.wikipedia.org/wiki/層_(数学) (2023/12/27 閲覧).

執筆者

NTTアドバンステクノロジ株式会社
デジタルAI事業本部　アドバンスデータアナリシスビジネスユニット
下川信祐（しもがわしんすけ）

略歴
大学で数学の専門教育を受け、難解な物理学が数学で明快に美しく捉えられることに感銘を覚えた。応用数学の新天地を目指して通信網の性能評価法の研究から業務をスタート。イノベーションに沿おうとする応用数学の取り組みが、モデルやデータを含めて、明快さ・美しさから乖離し強く複雑化する傾向が認められ、これを理解することが長期的なテーマとなった。以来、様々な業務を通じてこのテーマに取り組み、世界観が変わるような発見・気づきが継続的に得られ、世界の奥深さを感じてきた。現在は、分析業務に従事しつつ、パフォーマンスをコントロールできる汎用的な応用数学の方法論を目指している。

AIデータ分析コラム

このコラムは、NTT-ATのデータサイエンティストが、独自の視点で、AIデータ分析の技術、市場、時事解説等を記事にしたものです。
 

※本コラムの著作権は執筆担当者名の表示の有無にかかわらず当社に帰属しております。

 前のコラム    コラム一覧に戻る   次のコラム 

AIデータ分析シリーズ

• ソリューション
  • AIデータ分析コンサルティングサービス
  • 異常予兆検知ソリューション
  • 需要予測ソリューション
  • AI異常予兆検知ソリューション　＠DeAnoS
  • 電力使用量の見える化・需要予測ソリューション
  • 顧客行動分析ソリューション
  • 操業データ分析ソリューション
  
  

• パッケージ（TIBCO製品）
  • TIBCO Spotfire^®
  • TIBCO^® Data Science
  • TIBCO^® Streaming
  • TIBCO^® Data Virtualization

※DeAnoSは日本電信電話株式会社の登録商標です。
※当社とNTTコム オンライン・マーケティング・ソリューション(株)は、TIBCO Spotfireの販売契約を締結しています。
※TIBCOおよびSpotfireは、米国およびその他の国におけるCloud Software Group, Inc.およびその子会社の商標または登録商標です。